Wave mechanics

Basic Equation

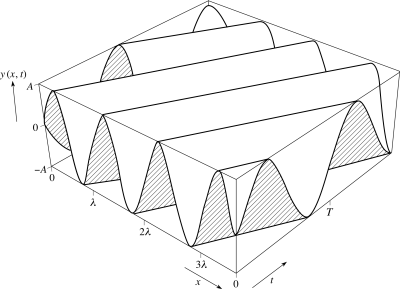
The basic equation of wave mechanics is a function that describes the position of a particle as a function of time and displacement, where the function is wavelike, such as sine or cosine:

y(x,t) = Ψ = Asin(kx - ωt)

A = amplitude

k = 2π/λ where λ = wavelength

w = 2πf = 2π/T where T = period

So if given the amplitude, wavelength and frequency of a particle that was behaving in a sine fashion, its position could be calculated at a particular time on the t axis using this equation. It would also give the particle position as a function of time at a particular distance on the x axis. Both plots y vs. x and y vs. t would be sine plots.

Partial Derivatives of basic wave equation

∂y/∂x = Akcos(kx-ωt)

∂y/∂t = -Aωcos(kx-ωt)

Second Partial Derivatives of basic wave equation

∂²y/∂x² = -k²Asin(ωt-kx)

∂²y/∂t² = -ω²Asin(ωt-kx)

so 1/k² ∂²y/∂x² = 1/ω² ∂²y/∂t²

or 1/k² ∂²y/∂x² - 1/ω² ∂²y/∂t² = 0

Wave Equation in One Dimension

since the speed of a wave (v) is equal to ω/k, the above equation can be expressed in terms of wave velocity by multiplying by ω²:

v² ∂²y/∂x² - ∂²y/∂t² = 0

or:

v² ∂²y/∂x² = ∂²y/∂t²

Solutions to Wave Equation in One Dimension

y(x,t) = F(x-vt) + G(x+vt)