Micro view of NMR
Contents
Quantum transitions in nuclei
In the micro view of NMR, it is an instrumental technique that uses photons of radio frequency energy to cause a transition, or change in state, in an atom. Radio is used because transitions at the atomic level are quantized, and the amount of energy needed to cause these transitions happens to fall in the radio region of the electromagnetic spectrum. Quantized energy means there has to be the right amount of energy to cause a change of state, too much or too little and no change occurs.
There are many quantum transitions in atoms, but the ones of interest in NMR are quantum spin transitions of protons and neutrons. Quantum spin in protons and neutrons has two states, which are normally equivalent, but when placed in a magnetic field they become non-equivalent, so adding the appropriate sized photon of energy can cause a transition from one to the other. This works fine for single protons and neutrons, but when these are combined into a nucleus the situation gets more complex and we have to rely on a net nuclear spin, called I.
Across the entire periodic table, net nuclear spin values ranging from I = 0 to I = 8 in ½-unit increments can be found. Protons and neutrons each have net spin of ½, but this derives from the elementary quarks and gluons of which they are composed. As a result of this complexity, no simple formula exists to predict I based on the number of protons and neutrons within an atom.
The formula for the number of states = 2I+1, thus a spin 1/2 nucleus such as a single hydrogen atom will have 2 states and 1 transition (when placed in a static magnetic field). For I greater than 1/2 there are more than two states and thus many transitions. The focus in NMR is on spin 1/2 nuclei since two states with one transition gives good, clean spectra that are easily interpretable. A lot of information about the environment of a nucleus can thus be obtained, making 1H NMR the most useful analytical technique in science.
From here on, the focus will be on spin 1/2 nuclei, specifically 1H. This nucleus is referred to as "proton" in the NMR literature, but other spin 1/2 nuclei behave the same. Nuclei with spins other than 1/2 will have more than one transition and give much more complicated spectra, so these will be explored in another section.
Spectra
To obtain a spectrum, a spin 1/2 atom must first be placed into a static magnetic field to cause separation of the two states. The amount of separation depends on the gyromagnetic ratio (gamma) (g) for that element (a constant) and the intensity of the static magnetic field (B0) according to the equation:
v0=g*B0
The atom is then pulsed with a composite radio wave that includes the frequency v0, called the Larmor Frequency. The atom absorbs just the v0 part of the radio wave (since it is a quantum transition), and a detector in the same axis as the radio wave (usually the same antenna) is then turned on to receive any emitted energy.
Making this happen in an instrument is thus mainly an engineering problem.
From the equation above, since g is a constant for each element and B0 is a constant (it is a measure of the magnetic field strength in that instrument in the units of Tesla), there is just one frequency for that proton, which makes sense since there is just one transition, thus there is just one peak expected in the spectrum. In reality though, an atom never exists in isolation, thus it never experiences the pure B0. The actual frequency v is thus slightly different for atoms of a particular g based on the actual magnetic field around the atom. These slight differences in frequency are what gives a spectrum of peaks for a molecule rather than a single peak. There is still just one transition for that atom type (if that type is spin 1/2, such as 1H), but the transition energy is different for each 1H that is in a different magnetic environment.
If the 1H is part of a molecule then 1H atoms in the molecule in similar magnetic environments can be grouped and can be expected to give one peak per group.
To see examples, the view will be increased beyond a single 1H atom and into a collection of 1H atoms as part of molecules, such as a solution of one compound in a solvent or a pure liquid, such as ethanol.
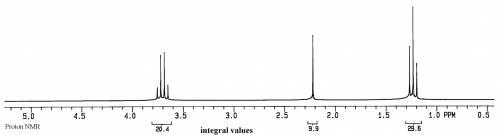
For a sample of ethanol (CH3CH2OH), we first have to list the spin 1/2 groups in the sample: 1H and 13C
- Fortunately, the g for 1H and 13C are very different, which means that the radio frequencies needed to cause spin transitions are also different. If a narrow band of radio is used both to transmit and receive, it is possible to "see" 1H and 13C separately. In other words, when looking at 1H, the 13C will not be excited because the quantum energy is not correct. The 13C are invisible in 1H spectra, and the 1H are invisible in 13C spectra.
Next is a listing of 1H groups in the sample:
A group for the protons in the CH3 of ethanol
A group for the protons in the CH2 of ethanol
A group for the OH of ethanol.
Thus three peaks are expected in the 1H spectrum of this sample.
The units on the x axis are ppm, which is relative frequency, while the y axis is relative intensity.
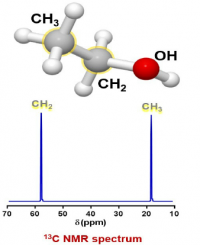
- Another spin 1/2 nucleus in this sample is carbon, specifically the 13C isotope. Based on the isotope abundance table, 13C is only 1.11% of the total carbon atoms in a sample. The other carbon atoms have spin 0 and are not visible in NMR, so, if the instrument is sensitive enough, it can detect the 1.1% of carbons in a sample that are spin 1/2.
A list of possible 13C carbons in the sample:
A group for the CH3 of ethanol
A group for the CH2 of ethanol.
There are no other carbon sources in this sample so there should be just 2 peaks in the spectrum.
Again, the units on the x axis are ppm, which is relative frequency, while the y axis is relative intensity. The ppm range is different than for the proton NMR spectrum because the g is different for the two nuclei, which makes the v0 different.
Radio pulse power
How powerful should the radio pulse be to get a good signal? Each transition requires one photon, so enough photons are needed in a pulse to cause transitions in all the nuclei in a sample. The total number of photons in a pulse of radio is the power of the pulse times the length of time that the pulse is turned on, where power is given in watts (W) and time in microseconds (µ). It is then a simple matter of running multiple experiments using different power and time settings until the maximum signal is achieved. The ideal numbers are actually limited by technical problems such as transmitter parameters and timing capabilities.
Saturation
Since NMR looks at quantum transitions of nuclei, only at absolute zero will all the nuclei be in the lowest energy state (not sure about that, need to check). At other temperatures there is a population in both states, with a slight excess in the lower energy state. The equation describing this is called the Bolztmann equation, which holds at thermal equilibrium:
(number of nuclei in the higher state)/(number of nuclei in the lower state) = e-(difference in energies/a constant*absolute temperature)
An NMR signal is only obtained when there is emission of a photon, so only the slight excess in the lower state is 'available' for excitation and subsequent emission of a photon. Thus as more and more photons are included in the pulse, at some point the populations will equalize and there will be no more transitions and no more signal. Then, as more photons are added the populations will invert, making the higher energy state slightly more populated. This will 'invert' the phase of the photons that are emitted after excitation.
Peak Intensity
So far there has been no discussion of how big the peaks are. Since there is one photon absorbed per nuclear transition, if photons could be counted then it would give the number of nuclei in the sample (subject to boltzmann distribution describe in the saturation section). Photon counts are represented by areas of peaks in spectra. This makes NMR a potentially quantitative method. The complication is that it is assumed that all excited nuclei release their photons at the same time so that the detector can see them. For 1H NMR this is mostly true, but for other nuclei it is not true since other factors such as delay in photon emission depending on the environment causing it to no longer be quantitative.
Sensitivity
Since this technique involves photon absorption by individual nuclei, the more nuclei in the sample the stronger the signal. For 1H, all protons in a natural abundance sample are 1H and thus all are available for excitation.
Peak Splitting
All the spins in a molecule can be considered a system, including the spins of the electrons that connect the nuclei. As a quantum system, the entire state, the state of each spin in the system, must be looked at to determine the status of the molecule at a particular time.