Difference between revisions of "Wave mechanics"
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
==Introduction== | ==Introduction== | ||
| − | Wave mechanics studies the properties of wave functions. These are periodic functions that carry information due to their periodic nature. The best way to study a function is to see how it changes, which can be done using derivatives, or derivatives of derivatives. | + | Wave mechanics studies the properties of wave functions. These are periodic functions that carry information due to their periodic nature. The best way to study a function is to see how it changes, which can be done using derivatives, or derivatives of derivatives. Wave mechanics are general and need have no physical interpretation. Real systems that behave as waves can be modeled with wave mechanics, but as with all real systems, there are complexities that are not captured by the math. These complexities can be approximated using [[Perturbation Theory]]. |
==Basic Equation== | ==Basic Equation== | ||
| Line 13: | Line 13: | ||
k = 2π/λ where λ = wavelength | k = 2π/λ where λ = wavelength | ||
| − | + | ω = 2πf = 2π/T where T = period | |
So if given the amplitude, wavelength and frequency of a particle that was behaving in a sine fashion, its position could be calculated at a particular time on the t axis using this equation. It would also give the particle position as a function of time at a particular distance on the x axis. Both plots y vs. x and y vs. t would be sine plots. | So if given the amplitude, wavelength and frequency of a particle that was behaving in a sine fashion, its position could be calculated at a particular time on the t axis using this equation. It would also give the particle position as a function of time at a particular distance on the x axis. Both plots y vs. x and y vs. t would be sine plots. | ||
| Line 31: | Line 31: | ||
∂<sup>2</sup>y/∂t<sup>2</sup> = -ω<sup>2</sup>Asin(ωt-kx) | ∂<sup>2</sup>y/∂t<sup>2</sup> = -ω<sup>2</sup>Asin(ωt-kx) | ||
| − | so 1/k<sup>2</sup> ∂<sup>2</sup>y/∂x<sup>2</sup> = 1/ω<sup>2</sup> ∂<sup>2</sup>y/∂t<sup>2</sup> | + | so 1/k<sup>2</sup> ∂<sup>2</sup>y/∂x<sup>2</sup> = 1/ω<sup>2</sup> ∂<sup>2</sup>y/∂t<sup>2</sup> since -<sup>2</sup>Asin(ωt-kx) is common to both |
or 1/k<sup>2</sup> ∂<sup>2</sup>y/∂x<sup>2</sup> - 1/ω<sup>2</sup> ∂<sup>2</sup>y/∂t<sup>2</sup> = 0 | or 1/k<sup>2</sup> ∂<sup>2</sup>y/∂x<sup>2</sup> - 1/ω<sup>2</sup> ∂<sup>2</sup>y/∂t<sup>2</sup> = 0 | ||
| Line 43: | Line 43: | ||
v<sup>2</sup> ∂<sup>2</sup>y/∂x<sup>2</sup> = ∂<sup>2</sup>y/∂t<sup>2</sup> | v<sup>2</sup> ∂<sup>2</sup>y/∂x<sup>2</sup> = ∂<sup>2</sup>y/∂t<sup>2</sup> | ||
| + | |||
| + | which is the general wave equation in one dimension that is used to describe situations involving periodic behavior. | ||
==Solutions to Wave Equation in One Dimension== | ==Solutions to Wave Equation in One Dimension== | ||
| Line 52: | Line 54: | ||
y(x,t) = F(x-vt) + G(x+vt) | y(x,t) = F(x-vt) + G(x+vt) | ||
| + | |||
| + | where F and G are smooth functions. | ||
| + | |||
| + | We already know that y(x,t) = Ψ = Asin(kx - ωt) is a solution to the wave equation since this is the equation that we used to derive it. Thus there are many solutions but they all fit the form y(x,t) = F(x-vt) + G(x+vt). | ||
Latest revision as of 00:26, 27 May 2020
Contents
Introduction
Wave mechanics studies the properties of wave functions. These are periodic functions that carry information due to their periodic nature. The best way to study a function is to see how it changes, which can be done using derivatives, or derivatives of derivatives. Wave mechanics are general and need have no physical interpretation. Real systems that behave as waves can be modeled with wave mechanics, but as with all real systems, there are complexities that are not captured by the math. These complexities can be approximated using Perturbation Theory.
Basic Equation
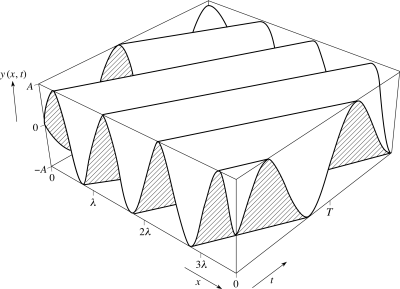
The basic equation of wave mechanics is a function that describes the position of a particle as a function of time and displacement, where the function is wavelike, such as sine or cosine:
y(x,t) = Ψ = Asin(kx - ωt)
A = amplitude
k = 2π/λ where λ = wavelength
ω = 2πf = 2π/T where T = period
So if given the amplitude, wavelength and frequency of a particle that was behaving in a sine fashion, its position could be calculated at a particular time on the t axis using this equation. It would also give the particle position as a function of time at a particular distance on the x axis. Both plots y vs. x and y vs. t would be sine plots.
Partial Derivatives of basic wave equation
Use a table of derivatives to find the derivatives of the basic wave equation with respect to x and time.
∂y/∂x = Akcos(kx-ωt)
∂y/∂t = -Aωcos(kx-ωt)
Second Partial Derivatives of basic wave equation
Use a table of derivatives to find the second derivatives of the basic wave equation with respect to x and time.
∂2y/∂x2 = -k2Asin(ωt-kx)
∂2y/∂t2 = -ω2Asin(ωt-kx)
so 1/k2 ∂2y/∂x2 = 1/ω2 ∂2y/∂t2 since -2Asin(ωt-kx) is common to both
or 1/k2 ∂2y/∂x2 - 1/ω2 ∂2y/∂t2 = 0
Wave Equation in One Dimension
since the speed of a wave (v) is equal to ω/k, the above equation can be expressed in terms of wave velocity by multiplying by ω2:
v2 ∂2y/∂x2 - ∂2y/∂t2 = 0
or:
v2 ∂2y/∂x2 = ∂2y/∂t2
which is the general wave equation in one dimension that is used to describe situations involving periodic behavior.
Solutions to Wave Equation in One Dimension
using fourier transform:
- multiply both sides by e-ikx
- integrate with respect to x
eventually end up with:
y(x,t) = F(x-vt) + G(x+vt)
where F and G are smooth functions.
We already know that y(x,t) = Ψ = Asin(kx - ωt) is a solution to the wave equation since this is the equation that we used to derive it. Thus there are many solutions but they all fit the form y(x,t) = F(x-vt) + G(x+vt).